|
|
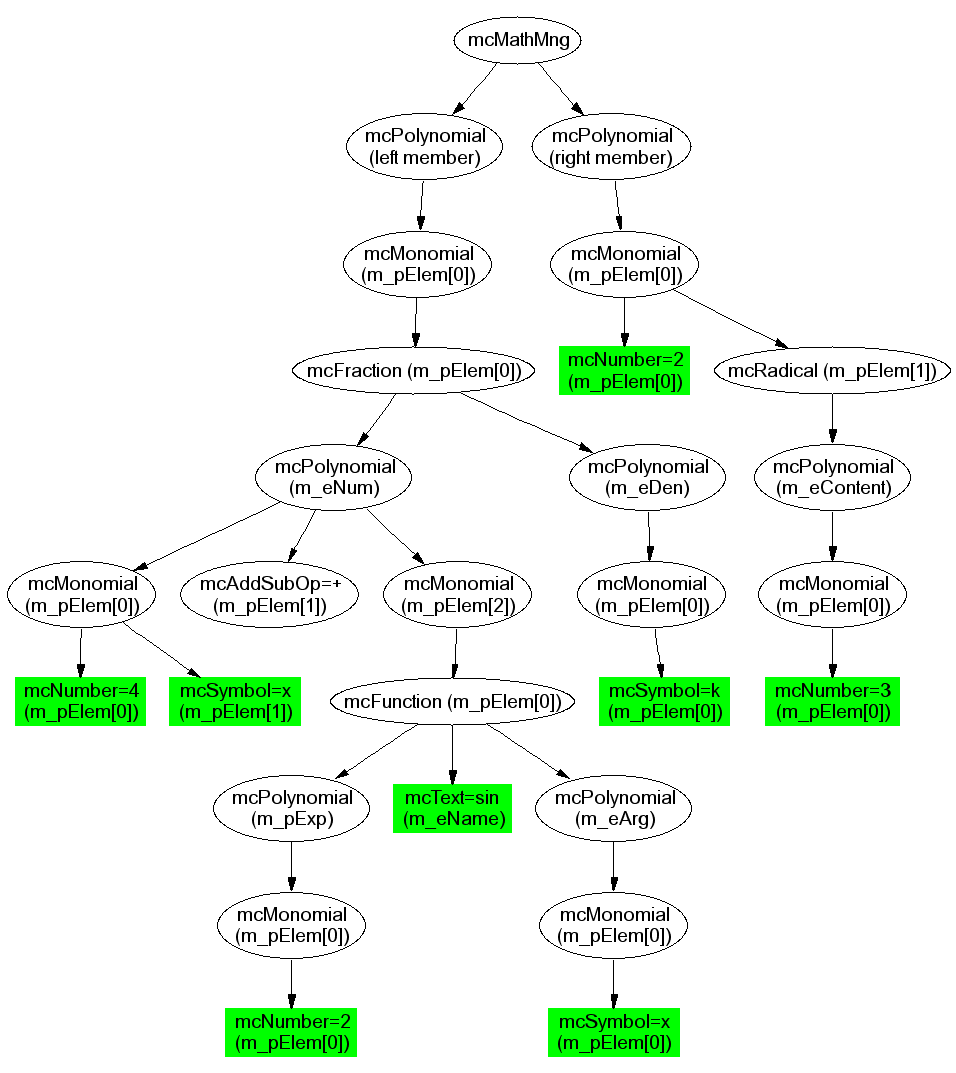
Every math expression can be considered a tree where the leaves are the smallest units (numbers, parameters, unknowns) and the other nodes are the containers of the leaves (brackets, fractions, radicals). This tree-structure is well-suited for a math library because it allows the creation of complex expressions using recursion (an example is shown later). Other approaches (like reverse polish notation) has already been tried, but they revealed to be too complex to handle or too complex to edit by math functions.
The following picture sums up the relations among main MathCore classes:
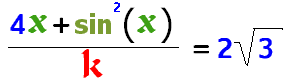
| On the left there is the graphical representation of the structure showed below. |
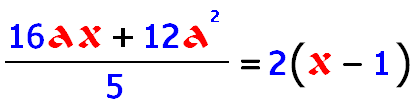
|
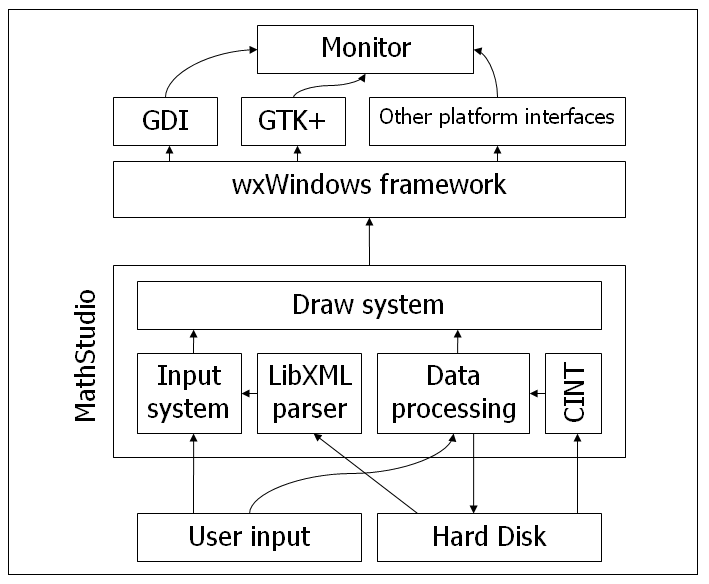
Why the math, IO, GUI subsystems are not kept as three separate libraries, each one specialized in its particular task ?
The three "subsections" of MathCore are all packed in a single library because, for example, it's very easier to create a flexible math library if we can create the math tree just sendind to the library a string representation of an inlined expression (that is, something like "4x+5^x-sin(x)")... in short, all the subsystem cooperates and make reciprocal tasks easier.
Why the sign operators (+ and -) are outside monomials ?
Keeping the mcAddOp and mcSubOp OUTSIDE mcMonomials, we can make very very easier mcMonomial GUI input system and, in addition, we can make the most of the mcElementArray class, which is designed as an array containing elements interleaved by operators (and if we keep the sign operators _inside_ monomials, we would not take advatange of this for mcPolynomials, which would contain only mcMonomials...). For math aspects, then it's true: the sign should be stored inside the monomials to make everything easier. To make a little sample: when mcPolynomials adds two mcMonomials then it should always check its sign to update accordingly the operator
Why do we use polynomials containing monomials and not directly polynomials containing elements ?
Polynomials containing directly the various elements like mcFractions, mcNumbers... was the first approach but, even if this solution makes input system easier to code, it was a real trouble for math system.
Why mcMathCore contains a lot of functions and variables which could be kept inside mcElementGUI as static elements ?
mcMathCore is planned to be only an allocator and the general mcElement class handler. Every other variable and function which can be placed as STATIC in mcElementGUI, mcElementMath, mcElementIO will be placed there.
[ Top ] |